CET ARTICLE EST PROTEGE PAR
IDDN. POUR AVOIR DES INFORMATIONS SUR LES DROITS D’AUTEUR, CLIQUEZ SUR CETTE
ICONE : ![]()
UN LIEN GEOMETRIQUE ENTRE LE CERCLE ET
LE SYSTEME SEXAGESIMAL
Par
Jaime Vladimir
TORRES-HEREDIA JULCA
(Université de Genève, Suisse)
1.- RESUME
Cet article présente un fait
géométrique simple qui pourrait concerner l’histoire des mathématiques et de
l’astronomie. Ce fait montre un lien naturel entre le cercle et les multiples de
6 et il permet d’obtenir une représentation simple des 12 mois de l’année, des
24 heures du jour, des 30 jours (nombre moyen) du mois et des 360 jours (nombre
approximatif) de l’année, ce qui nous rapproche de la division sexagésimale du
temps. Cette représentation rappelle d’ailleurs le mouvement des planètes
autour d’un centre.
A l’aide de ce fait on
pourra aussi trouver géométriquement les diviseurs principaux du nombre 60,
représenter des nombres en base 60 avec une sorte d’abaque ou table de calcul et
effectuer une division du cercle en 6 et 12 parties égales. Après on pourra
obtenir une division en 360 parties inégales mais relativement proches les unes
des autres, le but n’étant pas d’obtenir une division optimale du cercle en 360
parties égales mais de montrer que l’idée de partager le cercle en 360 parties
égales par la suite peut être suggérée par ces faits géométriques exposés.
Dans cet article l’auteur ne
répondra pas aux questions suivantes:
a)
Quelle est l’origine du système sexagésimal ?
b)
Par quel chemin pourrait-on arriver à adopter le
système sexagésimal à partir de la connaissance des faits exposés dans cet
article et à partir de la connaissance des données astronomiques ?
Ces questions pourraient
être traitées, à l’aide des informations de cet article, par les lecteurs ou
ultérieurement par l’auteur.
2.- INTRODUCTION
La division sexagésimale du
temps est largement utilisée tout comme la division sexagésimale du cercle pour
mesurer les angles. Or, on se demande souvent pourquoi on a adopté ces divisions. En fait, il est assez clair que l’adoption de
ce système est liée, entre autres, au besoin de représenter des données
astronomiques comme la durée de l’année (à peu près 360 jours).
Cependant,
comme cet article le montrera, la division sexagésimale du cercle et du temps a
des liens étroits avec un fait géométrique simple qui concerne le cercle et qui
est indépendant des données astronomiques.
Si ce fait géométrique n’a peut-être
pas, avec le besoin de représenter les 365 jours de l’année, contribué à faire
adopter le système sexagésimal employé pour diviser le cercle et représenter le
temps, au moins il peut servir à montrer un lien géométrique naturel entre le
cercle et la division sexagésimale.
3.- UN LIEN NATUREL ENTRE LE CERCLE ET LES NOMBRES
6, 12, 24, 30, 60 et 360
Un lien naturel entre le
cercle et les nombres 6, 12, 24, 30, 60 et 360 apparaît clairement lorsqu’on
observe comment un disque donné est entouré par d’autres disques de même rayon
successivement, en construisant des orbites juxtaposées autour du disque de
départ.
Voici le disque de
départ :

On entoure ce premier disque
avec 6 disques de même rayon. Les 6 nouveaux disques vont constituer une
« orbite » :

On répète le processus et
une deuxième orbite de 12 disques s’ajoute autour de la première orbite:

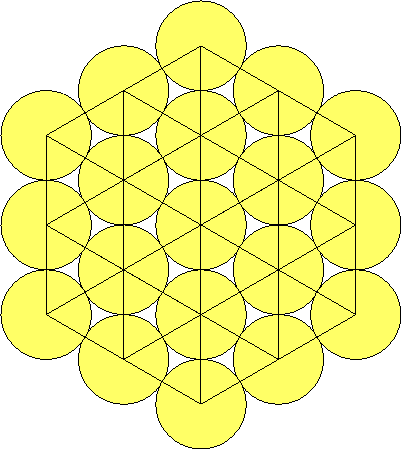
On peut remarquer que
lorsqu’on rajoute des orbites de disques de même rayon autour de celui de
départ, des « triangles équilatéraux » formés de disques se
constituent autour du centre. Ces triangles sont distingués ci-dessous par des
couleurs différentes :
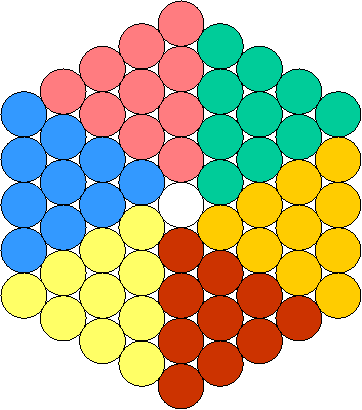
Plus il y a d’orbites, plus
les 6 « triangles équilatéraux » formés par des disques deviennent
grands. Et on remarque aussi qu’on peut trouver le nombre de disques d’une
orbite donnée en fonction du rang de l’orbite. Si l’on pose que r désigne le
rang d’une orbite et que r = 1 pour la première orbite, c’est-à-dire pour les
premiers 6 disques autour du disque de départ, alors le nombre N de disques
pour une orbite donnée est :
N = 6xr
Le nombre de disques d’une
orbite est donc un multiple de 6. Et si cette formule est correcte, l’orbite de
rang 60 aura 60x6 disques, c’est-à-dire 360.
Cette constatation nous
montre que les nombres 6, 12, 24, 30, 60 et 360 sont déjà liés de façon naturelle
au disque et au cercle parce que si on entoure un disque donné de la manière
proposée, on aura, à un moment donné 6, 12, 24, 30, 60 et 360 disques autour du
cercle de départ.
Il est clair qu’il y une
infinité d’orbites possibles puisqu’il y a une infinité de multiples de 6. Et
l’on peut choisir le 60ème
rang comme représentation des jours de l’année car l’avantage du nombre 360 est
qu’il est aussi multiple de 5 et de 10.
Par ailleurs, si l’on compte
les disques qui se trouvent dans les triangles colorés de la figure précédente,
on aura un total de 60, chaque « triangle équilatéral » ayant 10 disques. Donc il y a non seulement
60 disques mais encore la représentation de 6x10 = 60. Et les symétries de cette
figure permettent aussi de la diviser en 2 et 3 parties égales. Et comme chacun
des 6 « triangles équilatéraux » peut être divisé en 2 et 5 parties
égales (parce qu’ils contiennent 10 disques), on peut dire que le nombre 60 est
divisible par 2, 3 et 5 et aussi par 4. Autrement dit, cette figure montre les
diviseurs principaux du nombre 60. Et grâce à elle on peut aussi obtenir une
autre représentation géométrique du nombre 360 avec le total des disques
colorés ci-dessous:

On peut aussi représenter le
nombre 360 comme ça, toujours avec le total des disques colorés:

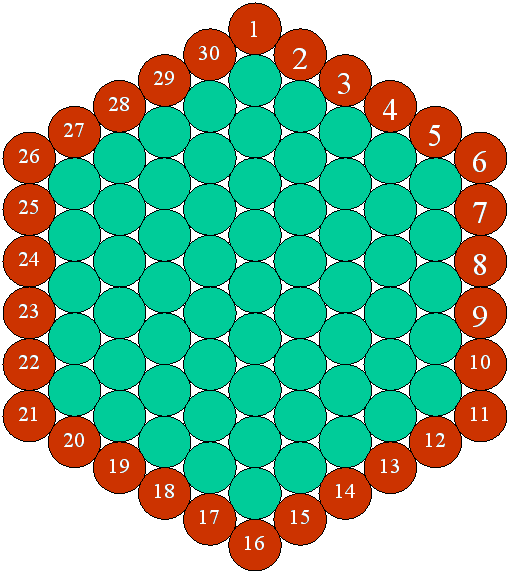
De plus, si l’on choisit le
système sexagésimal pour mesurer le temps,
on pourra représenter le nombre de mois d’une année avec une orbite de
12 disques, le nombre d’heures d’une journée avec une orbite de 24 disques, et
le nombre moyen de jours d’un mois avec une orbite de 30 disques, le tout d’une
façon qui rappelle le mouvement des planètes autour d’un centre.
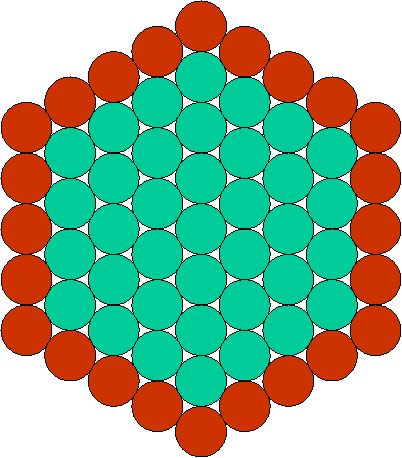
Voici une représentation des
douze mois de l’année avec des disques de couleur marron:
Les 24 heures du
jour avec des disques de couleur marron:
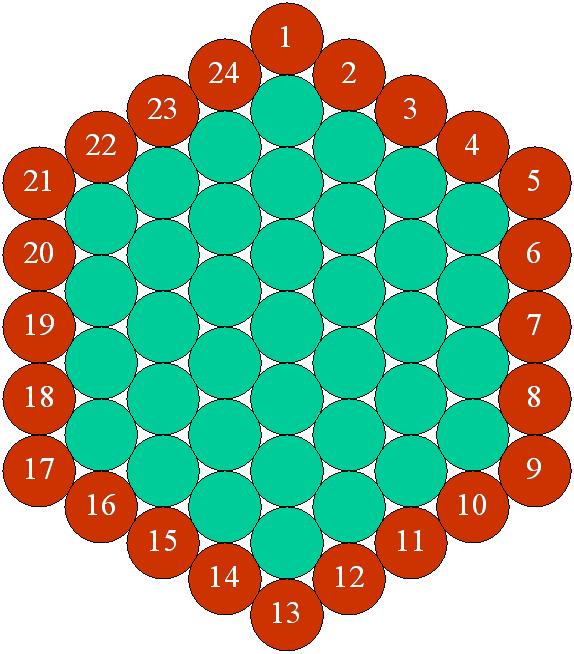
Les 30 jours d’un mois
(nombre moyen) :
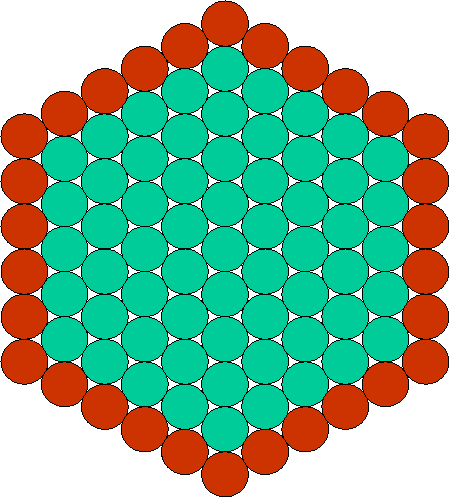
On pourrait aussi
représenter de cette façon le nombre approximatif de jours de l’année, i.e.
360.
Cette façon d’entourer les cercles
nous permet d’entrevoir une division du cercle en 360 parties du fait que le
nombre 360 est lié de façon naturelle, comme on l’a vu, au disque et au cercle.
4.- ABAQUE OU TABLE DE CALCUL EN BASE 60
Du fait qu’on peut
représenter le nombre 60 comme on l’a vu précédemment, on peut construire une
sorte de table de calcul ou abaque qui permettra de représenter les nombres en
base 60.
Voici le principe de cette table :

Le schéma
ci-dessus montre le poids qu’auraient des pièces comme des cailloux ou des
jetons placés sur les 6 « hexagones ». Et voici une représentation du
nombre 6’’’ 27’’ 49’ (en base 60):

En base
décimale ce nombre sera équivalent à :
6x602
+ 27x601 + 49x600 = 23269
Il est clair
qu’avec cette table on peut effectuer des sommes en réduisant les pièces d’un
hexagone rempli par une pièce de l’hexagone suivant comme on fait avec les
abaques de base décimale.
5.- DIVISION DU CERCLE EN 6 ET 12 PARTIES
EGALES :
On dessine d’abord un
triangle équilatéral.
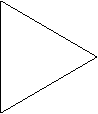
On juxtapose ensuite 5
autres triangles équilatéraux de même taille comme on le voit ci-dessous :
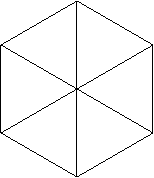
De la sorte on obtient un hexagone.
Puis, autour du centre de cet hexagone on va dessiner un cercle ayant comme
rayon la moitié de la longueur des côtés des triangles équilatéraux.
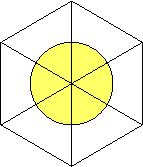
Il est clair maintenant que
le cercle est divisé en 6 parties égales, chaque partie étant délimitée par
l’un des rayons de l’hexagone. Ceci détermine aussi 6 angles égaux dont le
sommet est le centre du cercle.
Si l’on dessine d’autres
cercles de même rayon que le premier autour des sommets de l’hexagone, on obtiendra
la figure suivante, ce qu’on a vu plus haut, au point 3 :

Ensuite on peut rajouter des
triangles équilatéraux de même taille que les premiers de la façon
suivante :
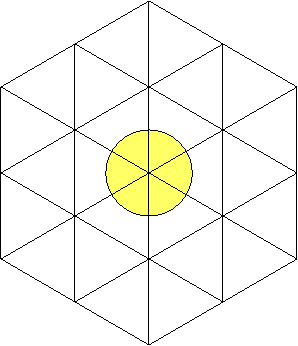
Comme auparavant, si on
dessine des cercles autour des sommets des triangles équilatéraux comme on le
montre ci-dessous, on obtient de nouveau la figure vue au point 3 de cet
article :
Ceci montre que cette
construction avec les triangles équilatéraux est liée à l’opération qui
consiste à ajouter des orbites de disques comme nous l’avons vu plus haut.
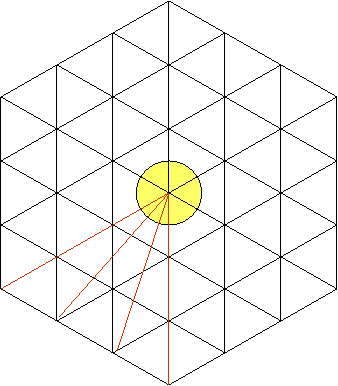
Maintenant, si l’on trace
trois rayons de couleur marron comme indiqué
ci-dessous, on observe que l’angle du cercle trouvé auparavant sera divisé en
deux parties égales à son tour. Ceci s’explique à l’aide des symétries et des
propriétés des triangles équilatéraux.
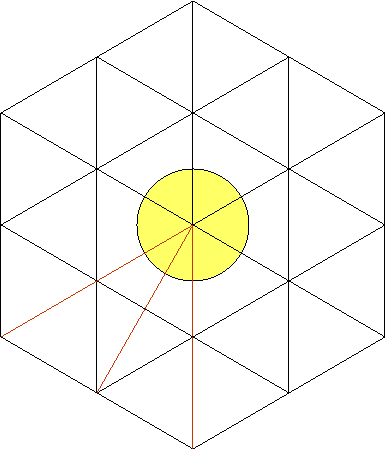
Comme ce processus peut être
appliqué au reste du grand hexagone, on peut affirmer qu’on a divisé le cercle
du centre en 12 parties égales et qu’on a trouvé 12 angles égaux :
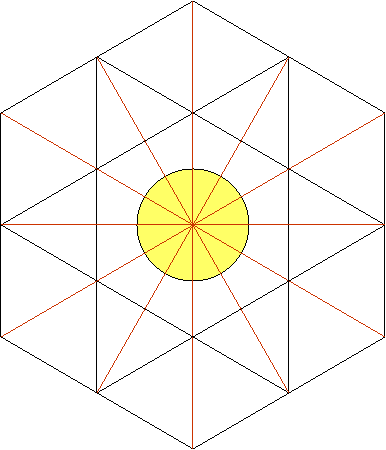
6.- DIVISION DU CERCLE EN 360 PARTIES INEGALES MAIS
RELATIVEMENT PROCHES LES UNES DES AUTRES
On peut évidemment encore
rajouter des triangles équilatéraux, comme on l’a fait jusqu’à présent, autour
de ceux qu’on a déjà dessinés :

Et encore une fois on peut
diviser les 6 angles de départ du cercle en d’autres parties, inégales cette
fois, comme on peut le constater ci-dessous :
Cette fois-ci on observe que
l’angle de départ a été divisé en 3 parties. Comme au départ il y avait 6
angles, on peut affirmer qu’on a divisé le cercle en 3x6=18 parties et qu’on a
trouvé aussi 18 angles mais inégaux.
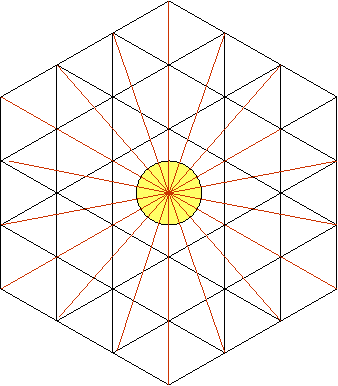
On peut continuer à rajouter
des triangles équilatéraux autour du dernier hexagone comme on la fait jusqu’à
présent mais on a pu déjà constater qu’il y avait toujours 6 grands triangles
équilatéraux composés de sous-triangles, équilatéraux eux aussi, autour du
centre du cercle. Voici les 6 grands triangles distingués par des traits
verts :
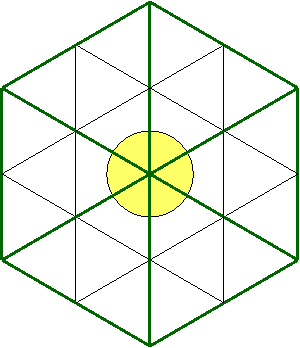
Voici les grands triangles
avec davantage de sous-triangles autour du cercle:
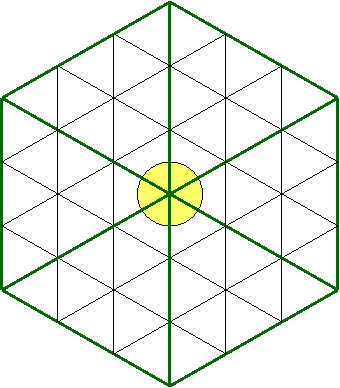
Le fait que les
sous-triangles équilatéraux, disposés comme on l’a proposé, se retrouvent à
l’intérieur d’autres triangles équilatéraux s’explique
aisément grâce encore une fois aux symétries et aux propriétés des triangles
équilatéraux.
On peut donc se concentrer
sur l’un des grands triangles équilatéraux afin de voir ce qui se passe par la
suite :
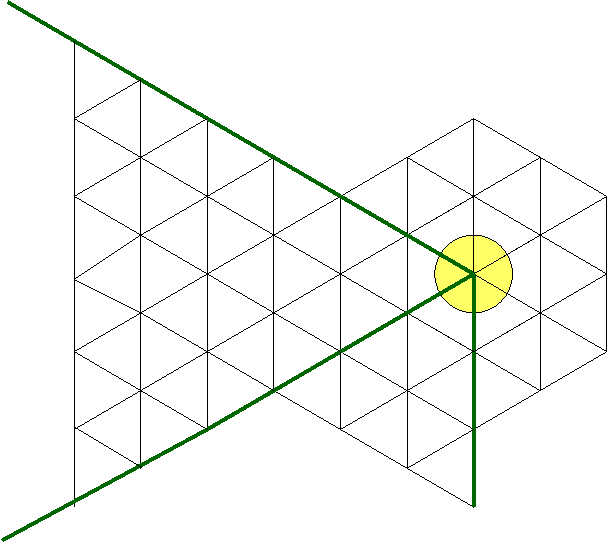
Comme on le remarque
ci-dessus, à chaque nouvel ajout de sous-triangles équilatéraux, selon la
méthode proposée, les 6 grands triangles délimités par les traits verts
augmentent d’un nombre impair de triangles. Et aussi, à chaque étape, on peut
diviser l’angle de départ en 2 parties, puis en 3, puis en 4, puis en 5, puis
en 6… :
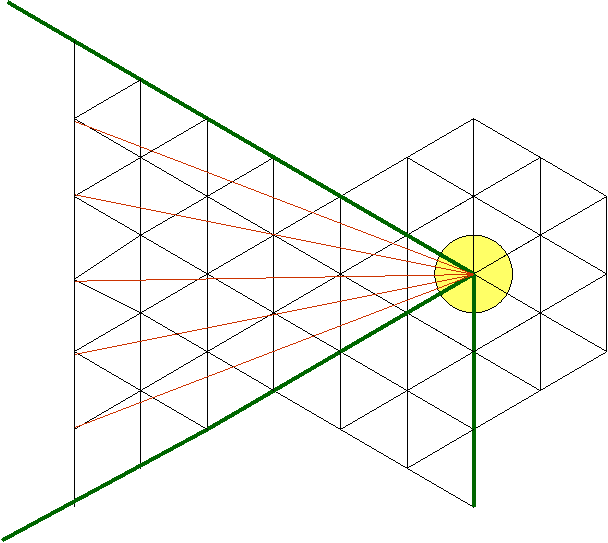
Ci-dessus il est montré
clairement que l’angle de départ a été divisé en 6 parties. Comme il y avait au
départ six angles égaux, on peut dire qu’on a trouvé de cette manière 6x6=36
angles inégaux. D’ailleurs, on peut conclure que le nombre de parties qu’on
obtient est un multiple de 6.
Si l’on poursuit le
processus, il est désormais clair qu’on arrivera à diviser l’angle de départ en
60 parties. Comme il y avait 6 angles égaux au départ, on aura divisé le cercle
en 60x6=360 parties inégales. De cette manière nous avons réussi à partager le
cercle en 360 parties de façon purement géométrique. Et il est clair désormais
que même si l’on n’obtient pas de parties égales, le partage du cercle en 360
parties est toutefois lié aux propriétés de base du cercle et du triangle
équilatéral. A partir de cette idée on peut essayer d’obtenir un partage en 360
égales comme ont essayé de faire les anciens Grecs.
Or, il faut remarquer que
même si les 360 angles obtenus précédemment sont inégaux, ils sont quand même
relativement proches des valeurs des angles égaux qui correspondent chacun à la 360ème
partie du cercle. En effet, on obtient lesdits angles inégaux par divisions
égales des 6 cordes correspondant aux 6 angles obtenus lors du premier partage
du cercle. En fait, la valeur de chacun des ces 360 angles inégaux obtenus avec
cette méthode varie entre à peu près 0.833883984 degrés et à peu près 1.10252169 degrés.
Pour mieux observer cela,
notons les angles obtenus par la manière décrite de la façon suivante :
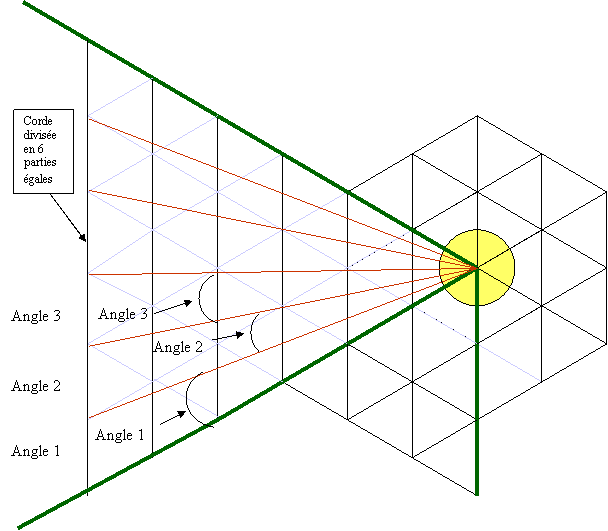
Le schéma ci-dessus montre à
quoi font référence les notations « Angle 1 », « Angle 2 »,
etc. qui se
trouvent à gauche du dessin. Ces notations font référence aux angles signalés
par les flèches et qui sont donc obtenus en reliant le centre du disque jaune
aux différents points de la corde qui a été divisée en 6 parties égales.
Ainsi qu’on l’a compris plus
haut, diviser des angles avec la méthode proposée revient à diviser une corde
correspondant à la 6ème partie d’un cercle en n parties égales et
ensuite relier au centre du cercle central chacun des points qui délimitent les
parties de la corde divisée. Or, afin de diviser le cercle en 360 parties, il
faut diviser une corde couvrant la 6ème partie en 60 parties. Mais
on peut aussi d’abord travailler avec la moitié du triangle équilatéral et
diviser la demi-corde en 30 parties. De cette façon on obtiendra les angles
suivants :
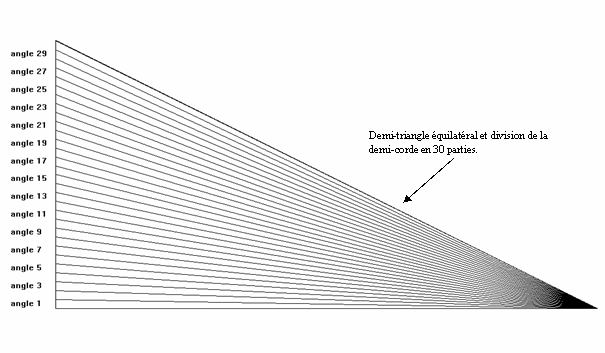
Et
maintenant nous pouvons voir les valeurs de ces angles qui sont numérotés. Sur
le tableau ci-dessous l’erreur absolue correspond à la différence entre l’angle
obtenu et l’angle théorique de 1 degré. L’angle parcouru correspond à l’angle
obtenu en superposant 60 fois chaque petit angle :
|
Angle |
Valeur en degrés |
Erreur absolue |
Erreur relative |
Arc parcouru |
|
1 |
1.10252169 |
0.10252169 |
9.299% |
66.1513014 |
|
2 |
1.101705813 |
0.101705813 |
9.232% |
66.1023488 |
|
3 |
1.100077676 |
0.100077676 |
9.097% |
66.0046606 |
|
4 |
1.097644472 |
0.097644472 |
8.896% |
65.8586683 |
|
5 |
1.094416892 |
0.094416892 |
8.627% |
65.6650135 |
|
6 |
1.090409009 |
0.090409009 |
8.291% |
65.4245405 |
|
7 |
1.085638123 |
0.085638123 |
7.888% |
65.1382874 |
|
8 |
1.08012458 |
0.08012458 |
7.418% |
64.8074748 |
|
9 |
1.073891559 |
0.073891559 |
6.881% |
64.4334935 |
|
10 |
1.066964833 |
0.066964833 |
6.276% |
64.01789 |
|
11 |
1.059372514 |
0.059372514 |
5.604% |
63.5623509 |
|
12 |
1.051144779 |
0.051144779 |
4.866% |
63.0686868 |
|
13 |
1.042313587 |
0.042313587 |
4.060% |
62.5388152 |
|
14 |
1.032912388 |
0.032912388 |
3.186% |
61.9747433 |
|
15 |
1.022975834 |
0.022975834 |
2.246% |
61.3785501 |
|
16 |
1.01253949 |
0.01253949 |
1.238% |
60.7523694 |
|
17 |
1.001639548 |
0.001639548 |
0.164% |
60.0983729 |
|
18 |
0.990312561 |
0.009687439 |
0.978% |
59.4187537 |
|
19 |
0.978595178 |
0.021404822 |
2.187% |
58.7157107 |
|
20 |
0.966523906 |
0.033476094 |
3.464% |
57.9914344 |
|
21 |
0.95413488 |
0.04586512 |
4.807% |
57.2480928 |
|
22 |
0.941463658 |
0.058536342 |
6.218% |
56.4878195 |
|
23 |
0.928545037 |
0.071454963 |
7.695% |
55.7127022 |
|
24 |
0.915412887 |
0.084587113 |
9.240% |
54.9247732 |
|
25 |
0.902100007 |
0.097899993 |
10.852% |
54.1260004 |
|
26 |
0.888638004 |
0.111361996 |
12.532% |
53.3182802 |
|
27 |
0.875057188 |
0.124942812 |
14.278% |
52.5034313 |
|
28 |
0.861386496 |
0.138613504 |
16.092% |
51.6831897 |
|
29 |
0.847653424 |
0.152346576 |
17.973% |
50.8592054 |
|
30 |
0.833883984 |
0.166116016 |
19.921% |
50.0330391 |
Evidemment,
plus on est proche de 1 degré, plus cet arc parcouru sera proche de 60 degrés.
Cette superposition peut aider à trouver l’angle le plus proche de 1 degré. Et
nous observons ainsi que le 16ème et 17ème angles sont
très proches de 1 degré.
La méthode présentée dans
cet article permet de diviser le cercle en 6 et 12 parties égales. Par division
simple en 2 avec le compas on peut encore diviser le cercle en 24, 48, 96, 192
et 384 parties égales.
Pour pourvoir atteindre une
division en 360 parties égales il faudrait d’abord diviser le cercle en 24 et
ensuite pouvoir diviser les angles en 3 et 5 parties car 360=24*3*5. Cela
suppose donc une méthode pour diviser en 3 ou en 5 l’angle correspondant à la
24ème partie du cercle, c’est-à-dire 15 degrés. Si l’on s’arrête à
12 angles au départ, il faudrait d’abord diviser un angle de 30 degrés en 3
parties et ensuite en 5 parties.
Or, on ne peut pas, à l’aide de la règle et du
compas, partager la plupart du temps un angle en 3 et 5 parties.
7.- L’étoile de David :
La façon d’entourer un
cercle par d’autres cercles comme on l’a vu au départ permet de dessiner
l’étoile de David :
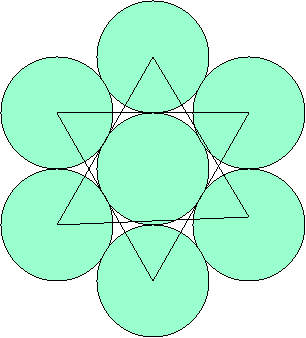
Pour cela il suffit de joindre
convenablement les centres des 6 cercles de la première orbite.
8.- Propriétés infinitésimales :
On a vu au point 3 que plus
on rajoutait d’orbites, plus on se rapprochait d’un hexagone formé de disques
de même rayon. On peut remarquer cela plus clairement grâce au schéma
ci-dessous :

Cela veut dire que si l’on
continue à rajouter des orbites indéfiniment tout en réduisant la taille des
disques afin que l’hexagone formé des disques soit inscrit dans un cercle de
rayon 1, on obtiendra cette forme « limite » :

Autrement
dit, on obtient un hexagone à partir d’une infinité de disques disposés de la
façon indiquée. Et cet hexagone-limite sera lui-même inscrit dans un cercle…
9.- Conclusions
Comme on l’a vu, ces faits
géométriques montrent qu’il y a un lien géométrique entre le cercle et le
système sexagésimal et que la division
du cercle en 360 parties égales, ce qui correspond à 360 angles égaux ou
degrés, n’est pas un choix totalement indépendant de la géométrie car cette
division peut être suggérée par les propriétés de base des cercles et des
triangles équilatéraux. En outre les faits géométriques exposés permettent de
représenter des données astronomiques d’une façon qui rappelle le mouvement des
planètes autour d’un centre. Et on a pu aussi représenter des nombres en base
60 grâce à ces propriétés du cercle et trouver géométriquement les diviseurs
principaux du nombre 60.
Il se peut que la façon de
représenter le temps, le partage tenté en 360 parties plus ou moins égales et
la représentation des nombres en base 60 exposés dans cet article aient joué un
rôle lors de l’adoption du système sexagésimal pour représenter les nombres,
diviser le cercle et représenter le temps.
10.- Commentaires
Cet article est la troisième
version de la présentation de ces faits géométriques. L’auteur prépare en ce
moment une autre version plus complète avec des calculs et avec des précisions
demandées par les lecteurs de cette version.
Version 3 du texte intitulé « UNE METHODE
NATURELLE POUR DIVISER LE CERCLE EN 360 PARTIES EGALES, CE QUI CORRESPOND A DES
DEGRES », écrit en janvier 2005.
Auteur: Jaime Vladimir TORRES-HEREDIA JULCA
Juillet 2005
Notes complémentaires au texte intitulé
« Un lien géométrique entre le cercle et le système sexagésimal »
écrit
par Jaime Vladimir TORRES-HEREDIA JULCA :
1.- A l’aide de des orbites vues au point 3 on
peut construire des
« hexagones » formés de cercles de même rayon de telles sorte qu’avec
six hexagones on aura 360 disques colorés (on ne compte pas les cercles du
milieu). Avec cela on peut construire donc un calendrier comme on le voit
ci-dessous :
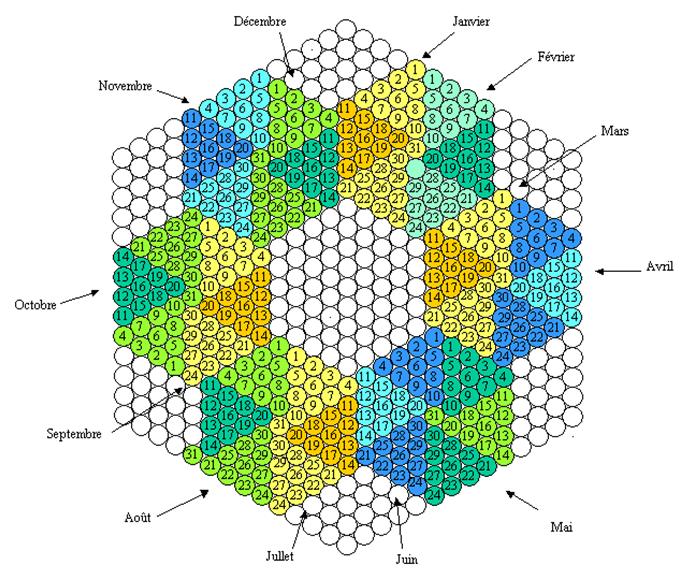
Le
mois sont distingués par les couleurs jaune, vert et bleu de telle sorte qu’on
distingue les groupes de 10 jours pour chaque mois.
© Jaime Vladimir TORRES-HEREDIA JULCA, juillet
2005.